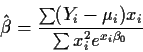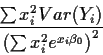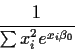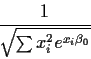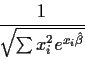Postscript version of these notes
STAT 350: Lecture 35
Estimating equations: an introduction via glm
Estimating Equations: refers to equations of the form
which are solved for 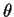 to get estimates
to get estimates
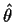 .
Examples:
.
Examples:
- 1.
- The normal equations in linear regression:
- 2.
- The likelihood equations:
where
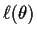 is the log-likelihood.
is the log-likelihood.
- 3.
- The equation which must be solved to do non-linear least squares:
- 4.
- The iteratively reweighted least squares estimating equation:
where, in a generalized linear model the variance
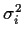 is a known
(except possibly for a multiplicative constant) function of
is a known
(except possibly for a multiplicative constant) function of 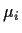 .
.
Only the first of these equations can usually be solved analytically.
In
Lecture 34
I showed you an example of an iterative technique of solving such equations.
Theory of Generalized Linear
Models
The likelihood function for a Poisson regression model is:
and the log-likelihood is
A typical glm model is
where the xi are covariate values for the ith observation
(often including an intercept term just as in standard linear
regression).
In this case the log-likelihood is
which should be treated as a function of 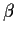 and maximized.
and maximized.
The derivative of this log-likelihood with respect to 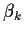 is
is
If 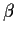 has p components then setting these p derivatives
equal to 0 gives the likelihood equations.
has p components then setting these p derivatives
equal to 0 gives the likelihood equations.
For a Poisson model the variance is given by
so the likelihood equations can be written as
which is the fourth equation above.
These equations are solved iteratively, as in non-linear
regression, but with the iteration now involving weighted least squares.
The resulting scheme is called iteratively reweighted least squares.
- 1.
- Begin with a guess for the standard deviations
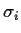 (taking them all equal to 1 is simple).
(taking them all equal to 1 is simple).
- 2.
- Do (non-linear) weighted least squares using the guessed weights.
Get estimated regression parameters
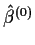 .
.
- 3.
- Use these to compute estimated variances
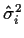 .
Go back to do weighted least squares with these weights and get
.
Go back to do weighted least squares with these weights and get
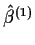 .
.
- 4.
- Iterate (repeat over and over) until estimates not really changing.
If the
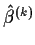 converge as
converge as
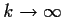 to something, say,
to something, say,
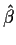 then since
then since
we learn that 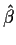 must be a root of the equation
must be a root of the equation
which is the last of our example estimating equations.
Distribution of Estimators
Distribution Theory is the subject of computing the distribution of statistics,
estimators and pivots. Examples in this course are the Multivariate Normal
Distribution, the theorems about the chi-squared distribution of quadratic forms,
the theorems that F statistics have F distributions when the null hypothesis
is true, the theorems that show a t pivot has a t distribution.
Exact Distribution Theory: name applied to exact results such as those in
previous example when the errors are assumed to have exactly normal distributions.
Asymptotic or Large Sample Distribution Theory: same sort of conclusions but
only approximately true and assuming n is large. Theorems of the form:
- An estimate is normally only useful if it is equipped with a measure of
uncertainty such as a standard error.
- A standard error is a useful measure of uncertainty provided the error of
estimation
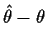 has approximately a normal distribution and the
standard error is the standard deviation of this normal distribution.
has approximately a normal distribution and the
standard error is the standard deviation of this normal distribution.
- For many estimating equations
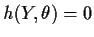 the root
the root
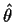 is unique
and has the desired approximate normal distribution, provided the sample size
n is large.
is unique
and has the desired approximate normal distribution, provided the sample size
n is large.
Sketch of reasoning in special case
POISSON EXAMPLE: p=1
Assume
Yi has a Poisson distribution with mean
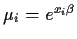 where
now
where
now 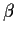 is a scalar.
is a scalar.
The estimating equation (the likelihood equation) is
It is now important to distinguish between a value of 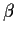 which
we are trying out in the estimating equation and the true value
of
which
we are trying out in the estimating equation and the true value
of 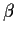 which I will call
which I will call 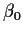 .
If we happen to try out the
true value of
.
If we happen to try out the
true value of 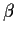 in U then we find
in U then we find
On the other hand if we try out a value of 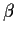 other than the
correct one we find
other than the
correct one we find
But 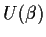 is a sum of independent random variables so by the law of
large numbers (law of averages) must be close to its expected value.
This means: if we stick in a value of
is a sum of independent random variables so by the law of
large numbers (law of averages) must be close to its expected value.
This means: if we stick in a value of 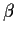 far from the right value
we will not get 0 while if we stick in a value of
far from the right value
we will not get 0 while if we stick in a value of 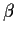 close to the
right answer we will get something close to 0. This can sometimes be
turned in to the assertion:
close to the
right answer we will get something close to 0. This can sometimes be
turned in to the assertion:
The glm estimate of 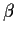 is consistent, that is,
it converges to the correct answer as the sample size goes to
is consistent, that is,
it converges to the correct answer as the sample size goes to 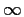 .
.
The next theoretical step is another linearization. If 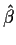 is the root of the equation, that is,
is the root of the equation, that is,
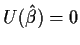 ,
then
,
then
This is a Taylor's expansion. In our case the derivative 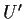 is
is
so that approximately
The right hand side of this formula has expected value 0, variance
which simplifies to
This means that an approximate standard error of 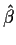 is
is
that an estimated approximate standard error is
Finally, since the formula shows that
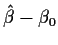 is a sum
of independent terms the central limit theorem suggests that
is a sum
of independent terms the central limit theorem suggests that 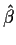 has an approximate normal distribution and that
has an approximate normal distribution and that
is an approximate pivot with approximately a N(0,1) distribution.
You should be able to turn this assertion into a 95% (approximate)
confidence interval for 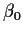 .
.
Scope of these ideas
The ideas in the above calculation can be used in many contexts.
- We can get approximate standard errors in non-linear regression.
- We can get approximate standard errors in any model where we
do maximum likelihood.
- We can show that the assumption of normal errors does not have
too big an impact on the t and F tests in multiple regression.
- We can get approximate standard errors in generalized linear models.
- We can demonstrate that the role of the Error Sum of Squares in
multiple regression can be replaced, approximately, by a function called
the Deviance which is a function whose derivative (with
respect to the parameters) is the estimating equation.
Further exploration of the ideas in this course
- STAT 402 explores applications of generalized models.
- STAT 410 applies regression to samples from finite populations.
- STAT 420 discusses the analysis of variance and regression
when the normality assumption seems very probably wrong.
- STAT 430 discusses the design and analysis of experiments.
Topics include: designs which save on effort by deliberately making
XTX singular, the advantages of randomized controlled experiments,
justification of t and F tests by randomization rather than sampling
arguments, experiments in which (some of) the
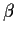 s are random.
s are random.
- STAT 450 discusses the exact and approximate distribution
theory discussed here, along with mathematical justifications for using
tests and estimates recommended here and in other courses as opposed
to any others.
- STAT 802 explores problems in which each Yi is
multivariate, that is, there is more than 1 response variable.
- STAT 804 (Time Series Analysis) explores problems
in which the errors
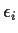 are not independent.
are not independent.



Richard Lockhart
1999-03-24
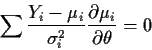
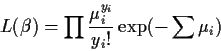
![]() is
is
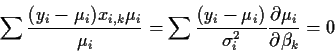
![]() converge as
converge as
![]() to something, say,
to something, say,
![]() then since
then since
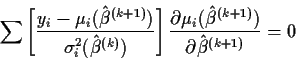
![\begin{displaymath}\sum
\left[\frac{y_i -\mu_i(\hat\beta)}{\sigma_i^2(\hat\beta)}\right]
\frac{\partial\mu_i(\hat\beta)}{\partial\hat\beta}
= 0
\end{displaymath}](img28.gif)
![]() where
now
where
now ![]() is a scalar.
is a scalar.
![]() is a sum of independent random variables so by the law of
large numbers (law of averages) must be close to its expected value.
This means: if we stick in a value of
is a sum of independent random variables so by the law of
large numbers (law of averages) must be close to its expected value.
This means: if we stick in a value of ![]() far from the right value
we will not get 0 while if we stick in a value of
far from the right value
we will not get 0 while if we stick in a value of ![]() close to the
right answer we will get something close to 0. This can sometimes be
turned in to the assertion:
close to the
right answer we will get something close to 0. This can sometimes be
turned in to the assertion:
![]() is consistent, that is,
it converges to the correct answer as the sample size goes to
is consistent, that is,
it converges to the correct answer as the sample size goes to ![]() .
.
![]() is the root of the equation, that is,
is the root of the equation, that is,
![]() ,
then
,
then