SAMPLE SIZE NEEDED using t test: SAND and FIBRE example.
Now for the same assumed values of the parameters how many replicates
of the basic design (using 9 combinations of sand and fibre contents)
would I need to get a power of 0.95? The matrix XTX for m replicates
of the design actually used is m times the same matrix for 1 replicate. This
means that
aT(XTX)-1a will be 1/m times the same quantity for
1 replicate. Thus the value of ![]() for m replicates will be
for m replicates will be
![]() times the value for our design, which was 2. With m replicates
the degrees of freedom for the t-test will be 18m-4. We now need to
find a value of m so that in the row in Table B 5 across from 18m-4degrees of freedom and the column corresponding to
times the value for our design, which was 2. With m replicates
the degrees of freedom for the t-test will be 18m-4. We now need to
find a value of m so that in the row in Table B 5 across from 18m-4degrees of freedom and the column corresponding to
Technically it would be pretty easy to imagine using 3.5 replicates - each combination of SAND and FIBRE would be tried 7 times giving 63-4=59 degrees of freedom for error. The achieved power would then be quite close to 0.95.
POWER of F test: SAND and FIBRE example.
Now consider the power of the test that all the higher order terms are
0 in the model
You will need to specify the non-centrality parameter for this Ftest. In general the noncentrality parameter for a F test
based on ![]() numerator degrees of freedom is given
by
numerator degrees of freedom is given
by
Now consider the sand and fibre example and assume
![]() ,
,
![]() and
and
![]() .
The following SAS code computes the required numerator.
.
The following SAS code computes the required numerator.
data plaster;
infile 'plaster.dat';
input sand fibre hardness strength;
newx = -0.004*fibre*fibre -0.005*sand*sand
+0.001*sand*fibre;
proc reg data=plaster;
model newx = sand fibre ;
run;
The output shows that the error sum of squares regressing newx on
sand, fibre and an intercept is 31.1875. Taking SAMPLE SIZE for F test: SAND and FIBRE example.
Now for the same basic problem and parameter values how many times would we
need to replicate the design to get a power of 0.95? Again the
non-centrality parameter for m replicates is m times that for 1
replicate; in terms of the parameter ![]() used in the tables the
value is proportional to
used in the tables the
value is proportional to ![]() .
With m replicates we now have
18m-6 denominator degrees of freedom. Again if 18m-6 is reasonably
large then we can use the
.
With m replicates we now have
18m-6 denominator degrees of freedom. Again if 18m-6 is reasonably
large then we can use the ![]() line and see that
line and see that ![]() must be
around 2.2 making m roughly 4 (
must be
around 2.2 making m roughly 4 (
![]() ).
).
Table B 12 can be used directly. Table 12 gives values
of n/r where n is the total sample size, the degrees of
freedom in the numerator of the F-test are r-1, the degrees of
freedom for error are n-r and the non-centrality parameter ![]() is given by
is given by
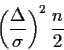
To use the table take ![]() .
Then work out
.
Then work out
![]() by taking
the value of the noncentrality parameter
by taking
the value of the noncentrality parameter
![]() for one replicate of
the basic design and computing
for one replicate of
the basic design and computing
In our example for a power of 0.95 and m replicates of the 18 point design we
have
![]() as above. We have r=3+1=4.
We get
as above. We have r=3+1=4.
We get
![]() .
For a level 0.05 test
we then look on page 1362 and get m=5 for a total sample size of 90. The degrees
of freedom for error will really be 84 but the table pretends that the degrees of
freedom for error will be
.
For a level 0.05 test
we then look on page 1362 and get m=5 for a total sample size of 90. The degrees
of freedom for error will really be 84 but the table pretends that the degrees of
freedom for error will be
![]() .
The latter is pretty small. The
table supposes a small number of error df which would decrease the power of a test.
This means that m=5 is probably an overestimate of the required sample size.
.
The latter is pretty small. The
table supposes a small number of error df which would decrease the power of a test.
This means that m=5 is probably an overestimate of the required sample size.
A better answer can be had by looking at replicates of the 9 point design. For
9 data points the nonecntrality parameter would have been
![]() .
This would give
.
This would give
![]() and m of 9 or 10. For m=10 we would have
the same design as before. For m=9 we would have only 72 data points. At this point
you go back to Table B 11 to work out the power properly for 72 or 80 data points and
see if 72 is enough.
and m of 9 or 10. For m=10 we would have
the same design as before. For m=9 we would have only 72 data points. At this point
you go back to Table B 11 to work out the power properly for 72 or 80 data points and
see if 72 is enough.
If plots and/or tests show that the error variances
![]() depend on i there are several standard
approaches to fixing the problem, depending on the nature
of the dependence.
depend on i there are several standard
approaches to fixing the problem, depending on the nature
of the dependence.
This usually arises realistically in the following situations:
If
![\begin{displaymath}\prod_{i=1}^n \frac{\sqrt{w_i}}{\sqrt{2\pi}\sigma}\exp\left[
-\frac{w_i}{2\sigma^2}(Y_i-x_i^T\beta)^2\right]
\end{displaymath}](img50.gif)
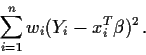
Algebraically it is easy to see how to do the minimization. Rewrite
the quantity to be minimized as
![\begin{displaymath}\sum_{i=1}^n \left[ w_i^{1/2} Y_i - ( w_i^{1/2}x_i)^T\beta\right]^2 \, .
\end{displaymath}](img53.gif)
It is possible to do weighted least squares in SAS fairly easily. As an example we consider using the SENIC data set taking the variance of RISK to be proportional to 1/CENSUS. (Motivation: RISK is an estimated proportion; variance of a Binomial proportion is inversely proportional to the sample size. This makes the weight just CENSUS.
proc reg data=scenic; model Risk = Culture Stay Nratio Chest Facil; weight Census; run ;
EDITED OUTPUT (Complete output)
Dependent Variable: RISK
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 5 12876.94280 2575.38856 17.819 0.0001
Error 107 15464.46721 144.52773
C Total 112 28341.41001
Root MSE 12.02197 R-square 0.4544
Dep Mean 4.76215 Adj R-sq 0.4289
C.V. 252.44833
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 0.468108 0.62393433 0.750 0.4547
CULTURE 1 0.030005 0.00891714 3.365 0.0011
STAY 1 0.237420 0.04444810 5.342 0.0001
NRATIO 1 0.623850 0.34803271 1.793 0.0759
CHEST 1 0.003547 0.00444160 0.799 0.4263
FACIL 1 0.008854 0.00603368 1.467 0.1452
EDITED OUTPUT FOR UNWEIGHTED CASE
(Complete
output)
Dependent Variable: RISK
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 5 108.32717 21.66543 24.913 0.0001
Error 107 93.05266 0.86965
C Total 112 201.37982
Root MSE 0.93255 R-square 0.5379
Dep Mean 4.35487 Adj R-sq 0.5163
C.V. 21.41399
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 -0.768043 0.61022741 -1.259 0.2109
CULTURE 1 0.043189 0.00984976 4.385 0.0001
STAY 1 0.233926 0.05741114 4.075 0.0001
NRATIO 1 0.672403 0.29931440 2.246 0.0267
CHEST 1 0.009179 0.00540681 1.698 0.0925
FACIL 1 0.018439 0.00629673 2.928 0.0042