


Postscript version of these notes
STAT 350: Lecture 17
Reading: There is no truly relevant part of the text except
chapter 5.
Summary of Last Time:
Suppose
Then
- 1.
- The covariance between X1 and X2 is
- 2.
-

- 3.
- In the regression model
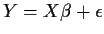 with
with
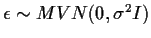
so that 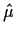 and
and
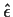 are independent.
are independent.
- 4.
- It follows that the Regression Sum of Squares (unadjusted)
(=
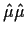 )
and the Error Sum of Squares (=
)
and the Error Sum of Squares (=
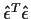 )
are independent.
)
are independent.
- 5.
- Similarly
so that 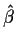 and
and
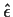 are independent.
are independent.
Conclusion:
is independent of
If we know that
then it would follow that
This leaves only the question: how do I know that
Recall: if
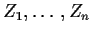 are iid N(0,1) then
are iid N(0,1) then
so we try to rewrite
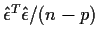 as
as
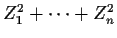 for some
for some
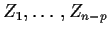 which are iid N(0,1). Here is how:
which are iid N(0,1). Here is how:
Put:
Then
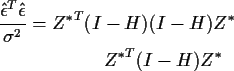
We are now going to define a new vector Z from Z* in such a
way that
- 1.
-
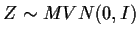
- 2.
-
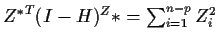
We use Eigenvalues and Eigenvectors to do so.
Eigenvalues, Eigenvectors, Diagonalization and Quadratic Forms
Linear Algebra theorem: If Q is an
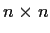 symmetric
(real) matrix then there are scalars
symmetric
(real) matrix then there are scalars
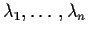 and
vectors
and
vectors
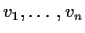 such that
such that
- 1.
-
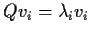 for each i. We call
for each i. We call 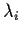 an
eigenvalue and vi a corresponding eigenvector.
an
eigenvalue and vi a corresponding eigenvector.
- 2.
-
viT vj = 0 for
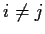 .
We say that the vectors
vi and vj are orthogonal.
.
We say that the vectors
vi and vj are orthogonal.
- 3.
-
viT v1 = 1. We say that vi is normalized.
Now make a matrix 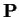 by putting the n vectors
by putting the n vectors
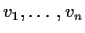 into
the columns of
into
the columns of 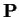 .
Then
.
Then 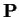 is an
is an
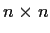 matrix. Next we
compute
matrix. Next we
compute
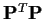 :
:
![\begin{align*}{\bf P}^T {\bf P} & = \left[\begin{array}{c} v_1^T \\ \vdots \\ v_...
...dots \\
0 & \cdots & 1 \end{array} \right]
\\
& = I_{ n \times n}
\end{align*}](img34.gif)
Thus
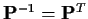 ;
;
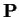 is a matrix whose inverse is just
its transpose. I remark that this proves that
is a matrix whose inverse is just
its transpose. I remark that this proves that
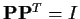 so that the rows of
so that the rows of 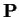 are orthonormal, just like the columns.
are orthonormal, just like the columns.
Now let
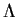 be the diagonal matrix whose entries along the diagonal
are
be the diagonal matrix whose entries along the diagonal
are
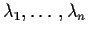 .
Then multiplying
.
Then multiplying
On the other hand
so
Multiply this equation on the right by 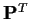 to conclude that
to conclude that
or on the left by 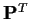 to conclude that
to conclude that
Rewriting a Quadratic Form as a Sum of Squares
Recall that we are studying
(Z*)TQZ* where Q is the matrix I-H and Z* is
standard multivariate normal. Replace Q by
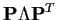 in this formula to get
in this formula to get
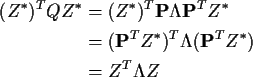
where
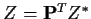 .
Notice that Z has a multivariate normal distribution whose
mean is obviously 0 and whose variance is
.
Notice that Z has a multivariate normal distribution whose
mean is obviously 0 and whose variance is
In other words Z is also standard multivariate normal!
Now look at what happens when you multiply out
Multiplying a diagonal matrix by Z simply multiplies the ith entry
in Z by the ith diagonal element so
Taking the dot product of this with Z we see that
We have rewritten our original quadratic form as a linear combination
of squared independent standard normals, that is, as a linear combination
of independent 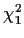 variables. This is the first big result:
variables. This is the first big result:
Theorem: If Z has a standard n dimensional
multivariate normal distribution and
Q is a symmetric
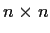 matrix then the distribution
of ZTQZ is the same as that of
matrix then the distribution
of ZTQZ is the same as that of
where the 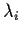 are the n eigenvalues of Q.
are the n eigenvalues of Q.
Now we turn to the conditions under which this linear combination of 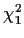 variables actually has a
variables actually has a
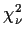 distribution and how to find
distribution and how to find 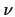 when it
does. The point is that
when it
does. The point is that
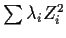 would have a
would have a
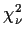 distribution
if the set of eigenvalues
distribution
if the set of eigenvalues 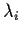 consisted of
consisted of 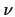 1s and all the rest were
0. How can we tell if an eigenvalue is 1 or 0?
1s and all the rest were
0. How can we tell if an eigenvalue is 1 or 0?
Suppose that each eigenvector vi has an eigenvalue 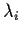 which is either 0 or 1.
Then notice that
which is either 0 or 1.
Then notice that
But 02=0 and 12=1 so
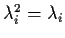 .
We then learn that
.
We then learn that
or
(Q2 - Q)vi = 0
for all i from 1 to n. Since the
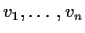 are a basis of Rn we have
proved that
are a basis of Rn we have
proved that
(Q2-Q)x=0
for every 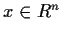 .
This guarantees that Q2=Q. Conversely suppose that
Q is a symmetric matrix such that Q2=Q, i.e. Q is idempotent. Then
the algebra above shows that
.
This guarantees that Q2=Q. Conversely suppose that
Q is a symmetric matrix such that Q2=Q, i.e. Q is idempotent. Then
the algebra above shows that
so that
for all i. The eigenvectors vi are not 0 so either
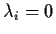 or
or
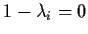 and
and
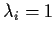 .
.
Theorem: The eigenvalues of a symmetric matrix Q are all either
0 or 1 if and only if Q is idempotent.
We have thus learned that
ZT Q Z has a 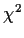 distribution provided that Q is idempotent. How can
we count the degrees of freedom? The degrees of freedom
distribution provided that Q is idempotent. How can
we count the degrees of freedom? The degrees of freedom 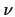 is just the number
of eigenvalues equal to 1. For a list of zeros and ones the number of ones is just
the sum of the list. That is
is just the number
of eigenvalues equal to 1. For a list of zeros and ones the number of ones is just
the sum of the list. That is
Finally, remember the properties of the trace and get
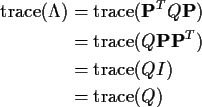
Application to Error Sum of Squares
Recall that
where
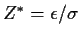 is multivariate standard normal.
The matrix I-H is idempotent so
is multivariate standard normal.
The matrix I-H is idempotent so
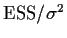 has a
has a 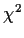 distribution with degrees of
freedom
distribution with degrees of
freedom 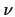 equal to
equal to
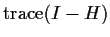 :
:
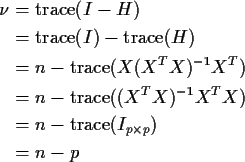
Quadratic forms, Diagonalization and Eigenvalues
The function
is a quadratic form. The coefficient of a cross product term
like x1x2 is
Q1,2+Q2,1 so the function is unchanged
if each of Q1,2 and Q2,1 is replaced by their average.
In other words we might as well assume that the matrix Q is
symmetric. Consider for example the function
f(x1,x2) = 6x12+3x22-4x1x2. The matrix Q is
What I did in class is the n-dimensional version of the following:
Find new variables
y1 = a1,1x1 + a1,2 x2 and
y2
= a2,1x1+a2,2 x2 and constants 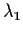 and
and 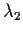 such that
such that
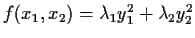 .
Put in
the expressions for yi in terms of the xi and you get
.
Put in
the expressions for yi in terms of the xi and you get
Comparing coefficients we can check that
where A is the matrix with entries ai,j and 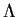 is
a diagonal matrix with
is
a diagonal matrix with 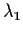 and
and 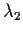 on the diagonal.
In other words we have to diagonalize Q.
on the diagonal.
In other words we have to diagonalize Q.
To find the eigenvalues of Q we can solve
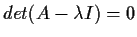 The characteristic polynomial is
The characteristic polynomial is
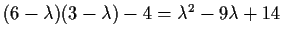 whose two roots are 2 and 7. To find the corresponding
eigenvectors you ``solve''
whose two roots are 2 and 7. To find the corresponding
eigenvectors you ``solve''
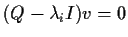 .
For
.
For
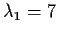 you get the equations
you get the equations
These equations are linearly dependent (otherwise the only solution would
be v=0 and 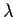 would not be an eigenvalue). Solving either one
gives v1=-2v2 so that (2,-1)T is an eigenvector as is any non-zero
multiple of that vector. To get a normalized eigenvector you divide through
by the length of the vector, that is, by
would not be an eigenvalue). Solving either one
gives v1=-2v2 so that (2,-1)T is an eigenvector as is any non-zero
multiple of that vector. To get a normalized eigenvector you divide through
by the length of the vector, that is, by 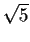 .
The second
eigenvector may be found similarly. We get the equation
2v2= 4v1 so
that (1,2)T is an eigenvector for the eigenvalue 2. After normalizing
we stick these two eigenvectors in the matrix I called P obtaining
.
The second
eigenvector may be found similarly. We get the equation
2v2= 4v1 so
that (1,2)T is an eigenvector for the eigenvalue 2. After normalizing
we stick these two eigenvectors in the matrix I called P obtaining
Now check that
This makes the matrix A above be PT and
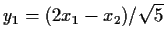 and
and
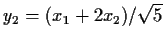 .
You
can check that
7y12 + 2y22 = 6x12+3x22 -4x1x2 as desired.
.
You
can check that
7y12 + 2y22 = 6x12+3x22 -4x1x2 as desired.
As a second example consider a sample of size 3 from the standard
normal distribution, say, Z1, Z2 and Z3. Then you know that
(n-1)sZ2 is supposed to have a 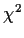 distribution on n-1 degrees
of freedom where now n=2. Expanding out
distribution on n-1 degrees
of freedom where now n=2. Expanding out
we get the quadratic form
2Z12/3 +2Z22/3 + 2 Z32/3 -2Z1Z2/3 - 2 Z1Z3/3 -2 Z2Z3/3
for which the matrix Q is
The determinant of
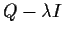 may be found to be
may be found to be
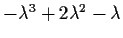 .
This factors as
.
This factors as
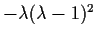 so that the eigenvalues are 1,
1, and 0. An eigenvector corresponding to 0 is
(1,1,1)T. Corresponding to the other two eigenvalues
there are actually many possibilities. The
equations are
v1+v2+v3 = 0 which is 1 equation
in 3 unknowns so has a two dimensional solution space.
For instance the vector
(1,-1,0)T is a solution.
The third solution would then be perpendicular to this,
making the first two entries equal. Thus
(1,1,-2)Tis a third eigenvector.
so that the eigenvalues are 1,
1, and 0. An eigenvector corresponding to 0 is
(1,1,1)T. Corresponding to the other two eigenvalues
there are actually many possibilities. The
equations are
v1+v2+v3 = 0 which is 1 equation
in 3 unknowns so has a two dimensional solution space.
For instance the vector
(1,-1,0)T is a solution.
The third solution would then be perpendicular to this,
making the first two entries equal. Thus
(1,1,-2)Tis a third eigenvector.
The key point in the , however, is that the distribution
of the quadratic form ZTQZ depends only on the eigenvalues
of Q and not on the eigenvectors. We can rewrite
2sZ2 in the form
(Z1*)2 + (Z2*)2. To find
Z1* and Z2* we fill up a matrix P with columns which
are our eigenvectors, scaled to have length 1. This makes
and we find
Z* = PT Z to have components
and
You should check that these new variables all have variance 1
and all covariances equal to 0.
In other words they are standard normals. Also check that
(Z1*)2 + (Z2*)2= 2sZ2.
Since we have written 2sZ2 as a sum of square
of two of these independent normals we can conclude that
2sZ2 has a 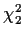 distribution.
distribution.



Richard Lockhart
1999-02-17
![\begin{displaymath}X = \left[\begin{array}{c} X_1 \\ \hline X_2 \end{array}\righ...
..._{12}
\\
\Sigma_{21} & \Sigma_{22} \end{array}\right]\right)
\end{displaymath}](img1.gif)
![\begin{displaymath}\left[
\begin{array}{c} \hat\mu \\ \hline \hat\epsilon \end{a...
...t[ \begin{array}{cc} H & 0
\\ 0 & I-H\end{array}\right]\right)
\end{displaymath}](img6.gif)
![\begin{displaymath}\left[
\begin{array}{c} \hat\beta \\ \hline \hat\epsilon \end...
...array}{cc} (X^TX)^{-1} & 0
\\ 0 & I-H\end{array}\right]\right)
\end{displaymath}](img11.gif)
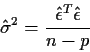
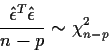
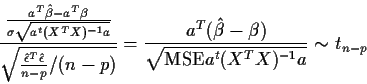
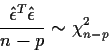
![]() are iid N(0,1) then
are iid N(0,1) then
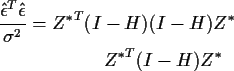
![]() symmetric
(real) matrix then there are scalars
symmetric
(real) matrix then there are scalars
![]() and
vectors
and
vectors
![]() such that
such that
![]() by putting the n vectors
by putting the n vectors
![]() into
the columns of
into
the columns of ![]() .
Then
.
Then ![]() is an
is an
![]() matrix. Next we
compute
matrix. Next we
compute
![]() :
:
![\begin{align*}{\bf P}^T {\bf P} & = \left[\begin{array}{c} v_1^T \\ \vdots \\ v_...
...dots \\
0 & \cdots & 1 \end{array} \right]
\\
& = I_{ n \times n}
\end{align*}](img34.gif)
![]() ;
;
![]() is a matrix whose inverse is just
its transpose. I remark that this proves that
is a matrix whose inverse is just
its transpose. I remark that this proves that
![]() so that the rows of
so that the rows of ![]() are orthonormal, just like the columns.
are orthonormal, just like the columns.
![]() be the diagonal matrix whose entries along the diagonal
are
be the diagonal matrix whose entries along the diagonal
are
![]() .
Then multiplying
.
Then multiplying
![\begin{displaymath}{\bf P}{\bf\Lambda} = \left[\begin{array}{ccc} v_1 & \cdots &...
...}{ccc}\lambda_1 v_1 & \cdots & \lambda_nv_n \end{array}\right]
\end{displaymath}](img38.gif)
![]() in this formula to get
in this formula to get
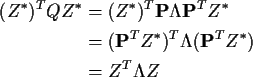
![]() .
Notice that Z has a multivariate normal distribution whose
mean is obviously 0 and whose variance is
.
Notice that Z has a multivariate normal distribution whose
mean is obviously 0 and whose variance is
![\begin{displaymath}{\bf\Lambda}Z = \left[ \begin{array}{c} \lambda_1 Z_1 \\ \vdots \\ \lambda_n Z_n
\end{array}\right]
\end{displaymath}](img49.gif)
![]() matrix then the distribution
of ZTQZ is the same as that of
matrix then the distribution
of ZTQZ is the same as that of
![]() variables actually has a
variables actually has a
![]() distribution and how to find
distribution and how to find ![]() when it
does. The point is that
when it
does. The point is that
![]() would have a
would have a
![]() distribution
if the set of eigenvalues
distribution
if the set of eigenvalues ![]() consisted of
consisted of ![]() 1s and all the rest were
0. How can we tell if an eigenvalue is 1 or 0?
1s and all the rest were
0. How can we tell if an eigenvalue is 1 or 0?
![]() which is either 0 or 1.
Then notice that
which is either 0 or 1.
Then notice that
![]() distribution provided that Q is idempotent. How can
we count the degrees of freedom? The degrees of freedom
distribution provided that Q is idempotent. How can
we count the degrees of freedom? The degrees of freedom ![]() is just the number
of eigenvalues equal to 1. For a list of zeros and ones the number of ones is just
the sum of the list. That is
is just the number
of eigenvalues equal to 1. For a list of zeros and ones the number of ones is just
the sum of the list. That is
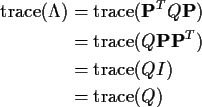
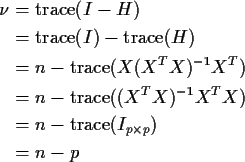
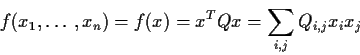
![\begin{displaymath}\left[\begin{array}{rr} 6 & -2 \\ -2 & 3 \end{array}\right]
\end{displaymath}](img74.gif)
![]() The characteristic polynomial is
The characteristic polynomial is
![]() whose two roots are 2 and 7. To find the corresponding
eigenvectors you ``solve''
whose two roots are 2 and 7. To find the corresponding
eigenvectors you ``solve''
![]() .
For
.
For
![]() you get the equations
you get the equations
![\begin{displaymath}P=\left[\begin{array}{rr}
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt...
...\\
\frac{-1}{\sqrt{5}}& \frac{2}{\sqrt{5}}
\end{array}\right]
\end{displaymath}](img88.gif)
![\begin{displaymath}P\Lambda^T P^T =
\left[\begin{array}{rr}
\frac{2}{\sqrt{5}} &...
...left[\begin{array}{rr} 6 & -2 \\ -2 & 3 \end{array}\right]
= Q
\end{displaymath}](img89.gif)
![]() distribution on n-1 degrees
of freedom where now n=2. Expanding out
distribution on n-1 degrees
of freedom where now n=2. Expanding out
![\begin{displaymath}Q = \left[\begin{array}{rrr}
2/3 & -1/3 & -1/3 \\
-1/3 & 2/3 & -1/3 \\
-1/3 & -1/3 & 2/3
\end{array}\right]
\end{displaymath}](img93.gif)
![\begin{displaymath}P = \left[\begin{array}{rrr}
\frac{1}{\sqrt{2}} & \frac{1}{\s...
...& \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{3}}
\end{array}\right]
\end{displaymath}](img97.gif)